El modelo de regresión lineal es ampliamente conocido y utilizado en diferentes aplicaciones que requieren de una predicción de una variable de salida (desconocida) en función de un conjunto de variables conocidas, con la premisa que la relación entre las entradas y la salida obedece a un patrón lineal.

Por otro lado, en la grandeza de su sencillez suelen quedar ocultos los detalles más bellos de este modelo. Es por esta razón que en esta entrada presentamos a este modelo desde una concepción probabilística que nos permitirá apreciarlo en todo su potencial.

Un modelo de aprendizaje supervisado

El regresor lineal, al intentar inferir una variable de salida en función de un conjunto de entrada, es claramente un modelo de aprendizaje supervisado, del cual, en nuestra entrada anterior se obtuvo una expresión general de distribución predictiva $p(y|\mathbf{x})$ que representa a estos modelos.

En el caso del regresor lineal se asume que la expresión anterior sigue una distribución normal con parámetros dependientes del vector de entrada $x$ . Esta decisión inicial nace del hecho que $y$ es una variable aleatoria continua que se cree es el resultado de la interacción entre otras variables. Luego, el teorema del límite central dice que la distribución de la variable resultante debe aproximarse a una gaussiana. De este modo:

$p(y|\mathbf{x}) = \mathcal{N}(y|\mu(\mathbf{x}),\sigma^2(\mathbf{x}))$

Quedando por definir $\mu(\mathbf{x})$ y $\sigma(\mathbf{x})$ que para el regresor lineal estas funciones toman la siguiente forma:

$\mu(\mathbf{x}) = \mathbf{w}^T \, \mathbf{x}$

$\sigma^2(\mathbf{x}) = \sigma^2$ , constante

Dado lo anterior, la distribución predictiva queda definida como:

$p(y|\mathbf{x}, \theta) = \mathcal{N}(y|\mathbf{w}^T \, \mathbf{x},\sigma^2)$

siendo $\theta$ el conjunto de parámetros $\{\mathbf{w},\sigma^2\}$ . De esta forma queda definido nuestro modelo predictivo del cual es necesario estimar sus parámetros $\theta$ .

Optimización de parámetros

Considerando que tenemos un conjunto $D=\{(y_1|\mathbf{x_1}),...,(y_N|\mathbf{x_N})\}$ y que no disponemos de ningún conocimiento inicial sobre la distribución de los parámetros, estos último pueden ser optimizados mediante el método de máxima verosimilitud descrito en nuestra entrada anterior con la siguiente función NLL:

$\begin{array} {lcl} NLL(\theta) & = & -\sum_{i=1}^{N} log \, p(y_i|\mathbf{x_i},\theta) \\ & = & -\sum_{i=1}^{N} log \, \mathcal{N}(y_i|\mathbf{w}^T \mathbf{x_i},\sigma^2) \end{array}$

Reemplazando la función gaussiana y simplificando:

$\begin{array} {lcl} NLL(\theta) & = & -\sum_{i=1}^{N} log \Big[ \frac{1}{\sqrt{2 \pi \sigma^2}} e^{\frac{-(y_i-\mathbf{w}^T \mathbf{x_i})^2}{2 \sigma^2}} \Big] \\ & = & -\sum_{i=1}^{N} log \big( \frac{1}{\sqrt{2 \pi \sigma^2}} \big) - \frac{(y_i-\mathbf{w}^T \mathbf{x_i})^2}{2 \sigma^2} \\ & = & -N \, log \big( \frac{1}{\sqrt{2 \pi \sigma^2}} \big) + \sum_{i=1}^{N} \frac{(y_i-\mathbf{w}^T \mathbf{x_i})^2}{2 \sigma^2} \\ & = & N \, log \sqrt{2 \pi \sigma^2} + \sum_{i=1}^{N} \frac{(y_i-\mathbf{w}^T \mathbf{x_i})^2}{2 \sigma^2} \\ & = & \frac{N}{2} \, log(2 \pi \sigma^2) + \frac{1}{2 \sigma^2} \sum_{i=1}^{N} (y_i-\mathbf{w}^T \mathbf{x_i})^2 \\ \end{array}$

Tomando la expresión anterior como la versión más simplificada de la función NLL, podemos definir el problema de optimización como:

$\hat{\theta}_{MLE} = \underset{\theta}{\mathrm{argmin}} \, \Big[ \frac{N}{2} \, log(2 \pi \sigma^2) + \frac{1}{2 \sigma^2} \sum_{i=1}^{N} (y_i-\mathbf{w}^T \mathbf{x_i})^2 \Big]$

Optimización de 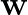$\mathbf{w}$

Primero consideremos la optimización del conjunto de parámetros $\mathbf{w}$ :

$\mathbf{\hat{w}}_{MLE} = \underset{\mathbf{w}}{\mathrm{argmin}} \, \Big[ \frac{N}{2} \, log(2 \pi \sigma^2) + \frac{1}{2 \sigma^2} \sum_{i=1}^{N} (y_i-\mathbf{w}^T \mathbf{x_i})^2 \Big]$

Eliminando los términos que no dependen de los parámetros o son constantes de normalización que no afectan al resultado de la optimización obtenemos:

$\mathbf{\hat{w}}_{MLE} = \underset{\mathbf{w}}{\mathrm{argmin}} \, \frac{1}{2} \sum_{i=1}^{N} (y_i-\mathbf{w}^T \mathbf{x_i})^2$

Si representamos las variables de entrada de las instancias en $D$ con la matriz $X \in \mathbb{R}^{N \times D}$ y la variable de salida con el vector $\mathbf{y} \in \mathbb{R}^N$ , podemos expresar de forma vectorial el problema de minimización:

$\mathbf{\hat{w}}_{MLE} = \underset{\mathbf{w}}{\mathrm{argmin}} \, \frac{1}{2} (\mathbf{y}-X\mathbf{w})^T \, (\mathbf{y}-X\mathbf{w})$

La función a optimizar es continua convexa, por tanto se puede resolver de forma exacta igualando a 0 su gradiente:

$\begin{array} {lcl} \nabla_\mathbf{w} \frac{1}{2} (\mathbf{y}-X\mathbf{w})^T \, (\mathbf{y}-X\mathbf{w}) & = & 0 \\ \nabla_\mathbf{w} \frac{1}{2} (\mathbf{y}^T-\mathbf{w}^T X^T) \, (\mathbf{y}-X\mathbf{w}) & = & 0 \\ \nabla_\mathbf{w} \frac{1}{2} (\mathbf{y}^T \mathbf{y} - \mathbf{y}^T X \mathbf{w} - \mathbf{w}^T X^T \mathbf{y} + \mathbf{w}^T X^T X \mathbf{w}) & = & 0 \\ \end{array}$

Un poco de carpintería:

$\begin{array} {lcl} \mathbf{y}^T X \mathbf{w} & = & (X \mathbf{w})^T \mathbf{y} \\ & = & \mathbf{w}^T X^T \mathbf{y} \end{array}$

Entonces el gradiente se simplifica a:

$\begin{array} {lcl} \nabla_\mathbf{w} \frac{1}{2} (\mathbf{y}^T \mathbf{y} - 2 \mathbf{w}^T X^T \mathbf{y} + \mathbf{w}^T X^T X \mathbf{w}) & = & 0 \\ \nabla_\mathbf{w} (\frac{1}{2} \mathbf{y}^T \mathbf{y} - \mathbf{w}^T X^T \mathbf{y} + \frac{1}{2} \mathbf{w}^T X^T X \mathbf{w}) & = & 0 \end{array}$

Luego de obtener el gradiente de cada término queda:

$X^T X \mathbf{w} - X^T \mathbf{y} = 0$

Y aparece la famosa ecuación normal del regresor lineal:

$X^T X \mathbf{w} = X^T \mathbf{y}$

Se puede apreciar que este es un sistema de ecuaciones de la forma $A \mathbf{x} = \mathbf{b}$ el cual para nuestro problema tiene la solución conocida como solución de mínimos cuadrados ordinaria:

$\mathbf{\hat{w}}_{OLS} = (X^T X)^{-1} X^T \mathbf{y}$

Optimización de 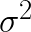$\sigma^2$

Comúnmente la optimización de este parámetro queda en segundo plano al no ser necesario para un modelo predictivo sin interpretación estadística. Sin embargo, aquí realizaremos la optimización de este parámetro logrando un resultado interesante:

$\hat{\sigma^2}_{MLE} = \underset{\sigma^2}{\mathrm{argmin}} \, \Big[ \frac{N}{2} \, log(2 \pi \sigma^2) + \frac{1}{2 \sigma^2} \sum_{i=1}^{N} (y_i-\mathbf{w}^T \mathbf{x_i})^2 \Big]$

Para resolver el problema de optimización procedemos igual que antes:

$\frac{\partial \Big[ \frac{N}{2} \, log(2 \pi \sigma^2) + \frac{1}{2 \sigma^2} \sum_{i=1}^{N} (y_i-\mathbf{w}^T \mathbf{x_i})^2 \Big]} {\partial \sigma^2} = 0$

Resolviendo el gradiente:

$\frac{N}{\sigma^2} - \frac{1}{(\sigma^2)^2}\sum_{i=1}^{N} (y_i-\mathbf{w}^T \mathbf{x_i})^2 = 0$

Dando como resultado:

$\hat{\sigma^2}_{OLS} = \frac{1}{N} \sum_{i=1}^{N} (y_i-\mathbf{w}^T \mathbf{x_i})^2$

Conclusiones

Habiendo obtenido $\theta$ , el modelo predictivo queda totalmente definido. La función de la media en si mismo representa el valor más probable de una distribución gaussiana, por lo que es la elección de preferencia para una predicción.

Por otro lado, el estimador obtenido para la varianza nos dice que la mejor estimación que podemos hacer sobre ella es la varianza de los datos.

Nótese que aquí solamente se considera MLE como método de optimización, pero MAP también es una opción resultando en el Regresor Ridge que esperamos abordar en una próxima entrada.

diegocabrera

Publicado

21 septiembre, 2018

por diegocabrera | 21 septiembre, 2018

La probabilidad detrás de la regresión lineal